Simulation Results of the forward movement of Mercury

Purpose

In this page the results of three simulations of the forward movement of the planet Mercury are discussed. The value of the angle is 574 arc sec per century.

Contents of this Page

Introduction
Simulation 1
Simulation 2
Simulation 3
Planet 3D results
Reflection
Feedback
Table 1, Simulation 1 and Simulation2
Table 2, Simulation 3

Introduction

The movement of the planet Mercury is an ellipse. The long axis of this ellipse does not stand still in space, but slowly moves forward in space.
The forward movement consists of three components:

The first component is caused by precession of the Earth Axis. The value is 5029 arc sec per century
The second component is caused by the influence of the other planets as described by Newton's Law. The value is 531 arc sec per century
The third component is explained by the Relativity Theory. The value is 43 arc sec per century

For the Geocentric (or Earth centered) co-ordinates of Mercury, all the three components are involved.
For the Heliocentric (or Sun centered) co-ordinates of Mercury, only the last two components are involved. This is the part that is simulated.
Of the three components only the sum is observed. The third value is a rest value, which is left over when the influence of the other two components is subtracted from observations.
In the following paragraphs the results of three simulations are shown. Each simulation starts when Mercury is at Aphelion or furthest away from the Sun. This is revolution 0.

In simulation 1 and 2 only component 2 is simulated. The final value should be 531 arc sec per century.
In simulation 3 the sum of the components 2 and 3 is simulated. The final value should be 574 arc sec per century.

The simulation takes into account that the plane of each planet, makes an angle (inclination) with the plane through the Earth and the Sun (Ecliptic).
Delta time for simulation 1 and 2 is 50 seconds. Delta time for simulation 3 is 100 seconds.

Simulation 1

The results of simulation 1 are shown in: Table 1, Simulation 1 and 2
Simulation 1 consists of the first four columns: rev, delta a, a and average a

The first column rev is the revolution number. This number is increased each time that Mercury goes through Aphelion.
The second column delta a shows the angle between two revolutions. The angle is expressed in arc sec per century.
The third column a shows the angle between revolution zero. The angle is expressed in arc sec per century.
The fourth column av(a) shows a running average of the forward movement.

The starting date for simulation 1 is:

10 March 1995, 9 hour, 17 min and 30 sec

The table is subdivided into two parts:

The first 20 arrays show the forward movement of the first 20 revolutions after the start of the simulation.
The second 20 arrays show the forward movement of the revolutions 400 to 420. Revolution 420 happens after approximate 100 years.

Simulation 2

The results of simulation 2 are shown in: Table 1, Simulation 1 and 2
Simulation 2 represents the last three columns.

Simulation 1 is almost the same as simulation 1, only the starting date is different. The starting date for simulation 2 is:

6 June 1995, 8 hour, 35 min and 58 sec

Which is the same date when simulation 1 reaches aphelion for the first time.

Simulation 1 and 2 are identical for the values in column 1.
Simulation 1 and 2 are not identical for the values in column 2 and 3.
The reason is because:
The first value in column 1 of simulation 1 is 3363.86. This value is not included in simulation 2.
The last value in column 1 of simulation 2 is -587.89. This value is not included in simulation 1.
The averaged difference is:

(3363.86 + 587.89)/420 = 9.41
The last value in column 2 of simulation 1 is 533.91
The last value in column 2 of simulation 2 is 524.91

The difference is 9.00

Simulation 3

The results of simulation 3 are shown in: Table 2, Simulation 3
The starting date for simulation 3 is the same as simulation 1. The difference between simulation 1 and 3 are the following:

The speed of the Sun in simulation 1 is 0 km/sec and in simulation 3 is 200 km/sec.
The direction of movement of the Sun is 180 degrees (away from Aphelion and towards Perihelion).
The speed of gravity propagation is 100 * c.
General Relativity Theory is not used.

The final value in the third column of simulation 3 should be equal to 574 arc seconds per century.
The reason of this difference can be:

The speed and direction of the Sun is different.
The speed of gravity propagation should be different and most probably be larger.

When the speed of gravity propagation is equal to c than the values in column 3 of simulation 3 are much larger.

The last value of simulation 3 column 3 is 618.81.
This value represents the final averaged value after 420 revolutions when the Sun moves away from Aphelion. This is 93.40 more than the final value 525.41 of simulation 1 column 3.
That is the maximum case.
In the opposite case the Sun would move towards Aphelion. The result of a simulation under those conditions gives a final average value of 430.41 arc seconds. This is 95.00 less than the final value 525.41 of simulation 1 column 3.
That is the minimum case.
This means many other values are possible including 574 arc sec per century.

Reflection

The most important aspect of simulation 1 and 2 is to demonstrate that it is difficult to calculate the forward movement of Mercury based on observations. The angle depents very much about the starting date and final date. To do this accurate a much longer period than 100 years is required.

The final value in the third column of simulation 1 (525.61) and 2 (518.14) should both have been equal to 531 arc seconds per century.
In order to improve the simulation one method is to increase the number of planets. One can divide each planet in two parts, which each half the mass of the original planet. The second planet of each is placed 180 degrees forward.
The forward angle after 420 revolutions in simulation 1 is than 529.04 arc seconds. The forward angle after 420 revolutions in simulation 2 is than 524.78 arc seconds.

The most important aspect of simulation 3 is to demonstrate that it is possible to simulate the movement of the planet Mercury without the Relativity Theory.
The most important assumption for this simulation is that the speed of gravity propagation is much larger than c.
For a more technical description see:The Reality, Now and Understanding

Planet 3D results

This paragraph shows the results of two simulations with the Visual Basic program "Planets3D".
For more technical information goto: PLANET.TXT . This is a chapter from the above mentioned e-book. Specific goto chapter 3: Mercury and Venus. In this chapter the influence of venus on the movement on the planet Mercury is explained.

Mercury and Venus
The following picture shows the forward movement of the planet Mercury caused by the planet Venus.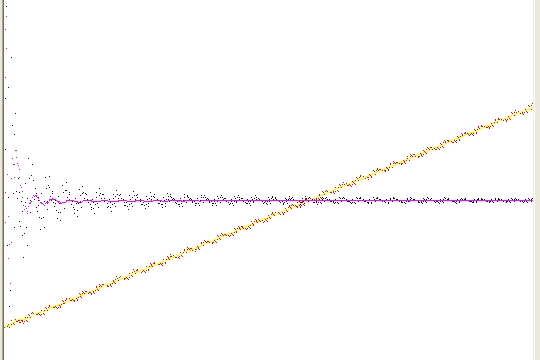

Picture 1A

The picure consists of two parts:
A more or less horizontal part and a second part under an angle of 45 degrees.
Each part consists of two lines.
In the horizontal part this are the blue line (dots) and the pink line.
In the 45 degree part this are the red line (dots) and the yellow line.
The simulation more or less starts the first time when Mercury reaches aphelion. (furtest distance). This defines angle 0.
The second time when Mercury reaches aphelion defines angle 1. The differences between angle 1 and angle 0 defines the first red dot (left bottom corner)
The third time when Mercury reaches aphelion defines angle 2. The differences between angle 2 and angle 0 defines the second red dot.
The fourth time when Mercury reaches aphelion defines angle 3. The differences between angle 3 and angle 0 defines the third red dot
This angle slowly increases, which explains the 45 angle.
The yellow line is more or less the same as the red line (dots), but now a more or less running averege is shown. (running squared distance).
The red dots define an angle as a function of a running time. The blue line defines also an angle but the time period is fixed i.e. 100 years. That is why the line of 45 degrees and the horizontal line cross each other at a distance 100 years after the origin. In this case this angle is 276.8 arc secs.
The pink line defines again the running average.
What is important to see that the forward movement angle is rather irregular. This is caused because the distance between Venus and Mercury is rather irregular. Specific the average distance during one revolution of Mercury depents very much on the average position of Venus. The influence is very different when Venus is on average closer to aphelion as to perihelion.
Mercury and 6 planets
The following picture shows the forward movement of the planet Mercury caused by the planets Venus, Earth, Mars, Jupiter, Uranus and Neptune.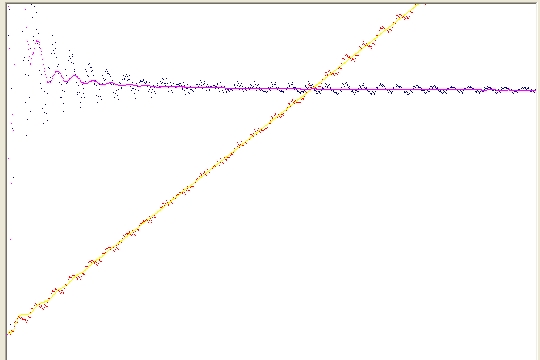

Picture 1B

In this particular case the forward movement is 533.1 arc sec in one century.

Feedback

None

Back to the: Contents of This Page

Table 1, Simulation 1 and 2

            simulation 1                   simulation 2         

Rev    delta a      a      av(a)      delta a      a       av(a)   
  0                0.0                                      
  1    3363.86  3363.86  3363.90                  0.0            
  2     335.95  1849.91  1849.92       313.81   313.81   313.81  
  3    -399.63  1100.07  1140.94      -353.13   -19.66   -19.66 
  4     246.71   886.73   875.03       325.99    95.56    57.83 
  5    3302.44  1369.87  1103.13      3127.86   853.64   609.54
  6     921.91  1295.21  1170.31       783.60   839.63   775.86
  7    -670.02  1014.47  1077.78      -652.37   590.97   706.50
  8    -352.88   843.55   961.24      -251.47   470.62   612.89
  9    1408.51   906.32   921.29      1557.30   606.45   617.66 
 10    -174.39   798.25   862.28      -290.78   506.76   581.62
 11    -995.27   635.21   774.75     -1040.94   351.99   505.47
 12   -1540.39   453.91   664.78     -1532.59   180.67   401.92
 13     689.70   472.04   595.69       833.82   235.10   349.09 
 14    1678.91   558.25   570.49      1854.24   359.65   347.32
 15    -952.28   457.55   529.31      -981.19   263.87   321.90
 16   -1925.82   308.59   466.01     -1956.12   115.87   268.04
 17   -1323.82   212.56   398.53     -1342.39    24.73   207.66
 18    2108.92   317.92   369.25      2288.32   157.89   191.16
 19    4057.99   514.77   385.70      4020.93   372.50   222.85
 20   -1110.38   433.51   384.45     -1130.95   293.37   232.55
                                     -1316.09   212.90   225.56
400    -455.71   529.08   525.22                            
401    4298.61   538.48   525.35      4189.17   531.65   518.51 
402    1635.48   541.21   525.51      1509.01   534.09   518.69 
403    -936.71   537.54   525.62      -919.47   530.47   518.82
404   -1116.90   533.45   525.70     -1074.88   526.49   518.91
405     280.97   532.82   525.77       361.21   526.08   519.00
406     802.11   533.49   525.85       676.16   526.45   519.09 
407    -716.81   530.42   525.89      -792.41   523.20   519.14 
408   -1223.36   526.12   525.89     -1233.10   518.89   519.16
409    -108.37   524.57   525.88       -19.80   517.57   519.16 
410     534.19   524.59   525.87       665.62   517.93   519.16
411    -747.67   521.49   525.82      -823.88   514.65   519.14 
412    -678.07   518.58   525.75      -734.71   511.61   519.08 
413    -924.61   515.09   525.65      -922.09   508.14   518.99
414    1133.07   516.58   525.56      1259.47   509.95   518.92 
415    3121.89   522.86   525.54      3221.45   516.50   518.91 
416     192.21   522.06   525.50       159.27   515.64   518.89 
417    -994.19   518.43   525.43     -1006.54   511.98   518.84 
418    -477.60   516.04   525.34      -483.63   509.60   518.77 
419    3797.18   523.88   525.33      3896.40   517.70   518.77
420    4737.21   533.91   525.41      4652.45   527.57   518.87 
421                                   -587.89   524.91   518.95

Back to the: Contents of This Page

Table 2, Simulation 3

         simulation 3 

Rev   delta a      a      av(a)    
  0               0.0                       
  1   3457.32  3457.32  3457.37
  2    429.40  1943.37  1943.39
  3   -306.16  1193.53  1234.40
  4    339.90   980.12   968.45
  5   3396.18  1463.34  1196.57
  6   1015.40  1388.68  1263.76
  7   -576.55  1107.94  1171.24
  8   -259.68   936.98  1054.69
  9   1501.04   999.66  1014.70
 10    -80.86   891.61   955.67
 11   -901.26   728.62   868.14
 12  -1447.17   547.31   758.18
 13    782.03   565.36   689.06
 14   1771.24   651.50   663.83
 15   -858.26   550.84   622.63
 16  -1831.73   401.94   559.34
 17  -1231.14   305.87   491.85
 18   2201.43   411.18   462.56
 19   4151.59   608.05   479.00
 20  -1016.87   526.80   477.75

400   -332.07   622.59   618.62
401   4353.64   631.89   618.75
402   1666.33   634.46   618.91
403   -847.61   630.79   619.02
404   -982.80   626.79   619.10
405    405.54   626.24   619.17
406    828.59   626.74   619.24
407   -657.66   623.59   619.28
408  -1093.57   619.38   619.28
409     -4.46   617.85   619.27
410    691.65   618.03   619.26
411   -686.27   614.86   619.22
412   -587.09   611.94   619.14
413   -862.82   608.37   619.04
414   1298.98   610.04   618.95
415   3263.51   616.43   618.93
416    271.05   615.60   618.90
417   -937.53   611.88   618.83
418   -369.65   609.53   618.74
419   3947.11   617.50   618.73
420   4764.98   627.37   618.81

Back to the: Contents of This Page

Created: 31 August 1996
Modified: 10 Mai 2002
Updated: 14 October 2015
Back to my home page: Contents of This Document

Simulation Results of the forward movement of Mercury

Purpose

Mercury and Venus

Mercury and 6 planets