|
|
|
|
|
As of 21 oktober 2023 perform the following:
In order to test the accuracy of the simulation use the CAMB Web Interface: https://lambda.gsfc.nasa.gov/toolbox/camb_online.html This page shows the following text: The CAMB online tool is currently unavailable while we upgrade it to a more recent version of CAMB and get it working on a new server operating system. This implies that this Tool does not work. The calling url is: https://lambda.gsfc.nasa.gov/toolbox/ Select CAMB |
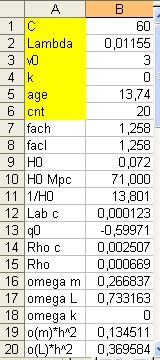
The results are: Age of the Universe = 13.707, Omega_M = 0.267011 and Omega_Lambda = 0.732989

|

|

|
|