Shor's Algorithm "Findprim shor.xls" Operation
Introduction and Purpose
The purpose of Shor's Algorithm is to do factorization on a Quantum Computer.
The purpose of the program "Findprim shor.xls" is to simulate Shor's algorithm on a personal computer or PC.
This document describes how to operate the Excel Program "Findprim shor".xls and the spreadsheets: "Shor", "Get Pr1" and "Get Pr2".
- Spreadsheet "Shor" simulates Shor's Algorithm in 6 steps to factorize 1 number
- Spreadsheet "Get Pr1" simulates Shor's Algorithm in 2 steps for 50 numbers.
- Spreadsheet "Get Pr2" simulates Shor's Algorithm in 2 steps for 1 number.
For a copy of the Excel program in zip format select: FINDPRIM SHOR.XLS
Contents
1. Spreadsheet layout: "Shor"
1.1 General Description Spreadsheet: "Shor"
- Spreadsheet "Shor" Contains the Commands: Factorize and End
- The command FactorizeEnd Command is displayed. The next paragragh gives a detailed description of the operation of the program.
- The Command Stop is used to stop the program. In most cases this command is only used when it is not possible to continue.
When the Stop is selected the Factorize is displayed and you can restart the program.
- "Shor" also contains three selection controls . The text of the controls can change. They are explained in the next paragraph.
- "Shor" also contains three Messages . The messages explain what to do or the results of the simulation.
The purpose of this example is to study as close as possible how a Quantum Computer operates, that means with a minimum of human intervention.
- In order to start the program, select the Factorize Command
- Input for the program are two (prime) numbers: pm1 and pm2. Multiplication of those two (prime) numbers gives a number n which is factorized using Shor's Algorithm. Those two numbers should be entered in the cells (1,B) and (2,B).
There are two ways to run the simulation:
- In 6 Steps. This is the standard method.
- In 2 Steps. If you want to do that you should select the 2 Steps Selection Control discussed later on.
In both cases, Input for the program are then two (prime) numbers
For example if you want to factorize 55, you should enter the numbers 5 and 11. An alternative way is to enter the two numbers 1 and 55.
When you enter 4 and 10 the nearest prime numbers are used/calculated which are 5 and 11
When one number is 1 the second number is not converted into a prime number.
For a description of all those 6 Steps see: http://www.uwyo.edu/moorhouse/slides/talk2.pdf
In this paragraph the example of page 18 is followed. That means you should enter the numbers 1 and 55 and select the Continue 1 Control
-
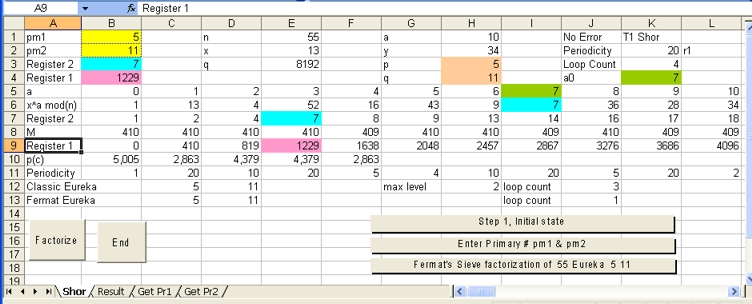
Next, as part of Step 1 the program displays the three calculated values n = pm1*pm2 in Cell (1,E) x in Cell (2,E) and q in Cell (3,E).
The values of q and x are calculated using the condition: 2n^2 < q = 2^x < 3n^2
The program displays the following Message: Option Enter x"
You can Enter a new value for x, if you want. If you do than a new value for q is calculated.
Select the Continue 2 Control
-
As part of Step 2 the results of x^a mod n is calculated in row 6 as a function of a, with a going from 0 to q - 1. The value of a is displayed in row 5.
It is important to observe that the values in row 6 repeats itself.
In this particular case (n = 55) the first number is a 1. The same value is at column "V", "AP", "BJ" and "CD". That means the same number 1 is in the columns 2, 22, 42, 62 and 82. In short, the periodicity r is 20
What is important is the number 34 in row 6 in column "L". This number is exactly in the middle between the two number 1 in the columns 2 and 22. The number 34 is important in Step 6 of Shor's Algorithm.
For more detail see: Shor's Algorithm - Answer Question 2
As part of step 2 an array of numbers is calculated how often each of the values (x^a mod n) is calculated. The values x^a mod n are displayed in row 7 and the array of numbers (the variable M) in row 8. In the program this array is called nxn(), explained in the next paragraph.
This means that row 6 and row 7 contain the same values. row 7 is also called Register 2
Because the periodicity can be easily calculated in this simple example, we have enough to calculate the two prime numbers 5 and 11, which are displayed in column "H".
This terminates the 2 Steps operation mode
Select the Continue 3 Control that means we follow the 6 Steps operation mode.
-
Step 3 is called Measure Register 2 and the following message is displayed: Select a number from Register 2 line
There are two ways to do that:
- Random. In that case the program selects a random number out of the numbers displayed in Register 2. If you want that to happen select Random
- User controlled. In that case select yourself a number out of row 7 and select: Select
Because we study the automatic mode, we select: Random.
The program selects in Register 2 in row 7 the number 2 in column "C", which changes into Cyan.
-
Step 4 starts with the following message: Discrete Fourier Transformation in Register 1
Together with this Message two selection controls are displayed: Continue 4 and Repeat Step 3
If you want to repeat the previous step: Select Repeat Step 3
In this particular case, automatic mode, we select: Continue 4
- Next as part of step 4 the following message is displayed: Observe FFT state values? together with three selection controls: ALL, Short 1 or Skip
- When you select ALL than all the FFT state values are displayed in sheet "Result"
- When you select Short 1 than only for those values c the FFT state value is displayed when this number is larger than the square root of M.
- When you select Skip there is no display
In this particular example we select: Skip
When All or Short 1 are selected, the Selection Control Continue 5 is also displayed
-
Next as part of step 4 the following message is displayed: Observe probability values? together with three selection controls: ALL, Short 2 or Skip
- When you select ALL than all the FFT probability values are displayed in sheet "Result"
- When you select Short 2 than only for those values c are displayed when the probability values (stored in array p(c)) are larger than 1/r
- When you select Skip there is no display
In this particular example we select: Skip
- in the final part of step 4 the probability values are calculated.
During this time the two controls Wait and Skip are displayed. When Skip is selected step 4 is forced to end.
At the same time a counter in percentage is displayed which shows how far we are.
When the 100% is reached the counter is cleared
Two messages are displayed:
- "Grand probability total = 100"
- "Probability total = 96.1735"
Which are explained in Example 2
This terminates step 4. Select Continue 6
-
Step 5 starts with the following message: Measure Register 1
Row 9 shows the same highest c values of the highest probability values. This is Register 1
Row 10 shows the corresponding probability values
Row 11 shows periodicity values which are explained later on
Together with the above message the following message is displayed:
- Select a number from Register 1 line
-
There are two ways to do that:
- Random. In that case the program selects a random number out of the numbers displayed in Register 1. If you want that to happen select Random
- User controlled. In that case there are three options:
- You can select self a number out of row 9 and select Select
- In case there is a short list displayed starting from row 20, you can select one of those values and select
Select
- You can select a value either way, modify the value and select Select. The purpose is to see what happens if values with smaller probabilities are selected.
In this particular case (automatic mode) we select Random
The program selects the value 6963 in column "N"
-
Step 6 starts with the following 3 messages:
- Continued Fraction Convergent of 6963. The value 6963 is the value selected at the end of Step 5
- In this particular case: Possible values for periodicity r, are multiples of r1 = 20
- In this particular case: GCD n = 55 a = 10 y = 34 p = 5 q = 11
Together with these the following messages are displayed (Also in the Debug buffer):
0 a = 0 p = 406 / 8192
1 a = 20 p = 72 / 406 Convergent 1 / 20
2 a = 5 p = 46 / 72 Convergent 5 / 101
3 a = 1 p = 26 / 46 Convergent 6 / 121
4 a = 1 p = 20 / 26 Convergent 11 / 222
5 a = 1 p = 6 / 20 Convergent 17 / 343
6 a = 3 p = 2 / 6 Convergent 62 / 1251
7 a = 3 p = 0 / 2 Convergent 203 / 4096
|
Accordingly to the text: "We stop before the denominator exceeds n=55", that means periodicity = 20.
Now a = 10. y = x^a mod n = 13^10 mod 55 = 34.
Finally you have two perform two calculations:
- GCD (y-1,n) = GCD(33,55) = 11
- GCD (y+1,n) = GCD(35,55) = 5
Together with this three Message two selection controls are displayed: Continue 7 and Repeat Step 5
If you want to repeat the previous step: Select Repeat Step 5
In this particular case, select: Continue 7
For details see document 1 mentioned above.
-
At the end the following message is displayed This terminates Shor's Algorithm simulation
Finally, the factorization results of Classical Algorithm and Fermat's sieve Algorithm are displayed in resp. row 12 and row 13.
In this case the Classical Algorithm requires 3 calculations Fermat's sieve Algorithm requires 1 Calculation.
In Example 1 we have performed the Automatic Mode. That means the logic of the program flow is controlled by the internal results of the Quantum Computer.
In this Example we are going to study what happens with more manual intervention. The same example is studied, however in this case we use pm1 = 5 and pm2 = 11.
- Select the command Factorize
- Enter pm1 = 5 and Pm2 = 11 and Select Continue 1
- Select Continue 2
- Select Continue 3
-
Step 3 is called Measure Register 2 and the following message is displayed: Select a number from Register 2 line. This is "row 7".
There are two ways to do that: Random or Select
In this particular case we select in row 7 the number 28 (This is column "N") and select Select
After this action the number 28 will change in "Cyan"
-
Step 4 starts with the following message: Discrete Fourier Transformation in Register 1
Together with this Message two selection controls are displayed: Continue 4 and Repeat Step 3
If you want to repeat the previous step: Select Repeat Step 3
In this particular case, select: Continue 4
- Next as part of step 4 the following message is displayed: Observe FFT state values? together with three selection controls: ALL, Short 1 or Skip
- When you select ALL than all the FFT state values are displayed in sheet "Result"
- When you select Short 1 than only for those values c the FFT state value is displayed when this number is larger than the square root of M.
- When you select Skip there is no display
In this particular case select All
The display shows a percentage counter.
When the counter reaches 100 select the spreadsheet results
What the display shows that the highest FFT state values are displayed is clusters.
Typical clusters are around c = 0, 410, 819 etc.
For more technical detail go to: Does FFT work?
Selection Control Continue 5 is displayed and selected.
-
Next also as part of step 4 the following message is displayed: Observe probability values? together with three selection controls: ALL, Short 2 or Skip
- When you select ALL than all the FFT probability values are displayed in sheet "Result"
- When you select Short 2 than only for those values c are displayed when p(c) is larger than 1/r
- When you select Skip there is no display
What the display shows that the most probable values displayed again are in clusters.
In this particular case with n = 55 select: Short 2
And compare the result with the display on page 20 in the above mentioned URL. Called: "Step 5: Measure Register 1"
In row 20, 25, 30 and 35 in row B you have the highest probability values of 5.005.
In row 21 (for c = 410) and in row 24 (for c = 1638) you have the highest probability values of 2.863. Those 2 values repeat itself four times. Those same values are also on the display of page 20
In row 22 (for c = 819) and in row 23 (for c = 1229) you have the highest probability values of 4.379. Those 2 values repeat itself four times. Those same values are also on the display of page 20
What this means is that the results of the simulation are in accordance with the above mentioned URL.
However not completely. The four highest values for c = 0, 2048, 4096 and 6144 do not match.
-
Next as part of step 4 the two messages "Grand probability total" and "Probability total" are displayed which each a value. In the case of n=55 the values are 100 and 96.17
The value of 100 means that the sum of all the probability values is 100%. This is as expected, which also indicates that the four values of 5.005 are correct.
This terminates step 4. Select Continue 6
-
Step 5 starts with the following message: Measure Register 1
Row 9 shows the same highest c values as displayed in red in the previous short list. This is Register 1
Row 10 shows the corresponding probability values
Row 11 shows periodicity values which are explained later on
Together with the above message the following message is displayed:
- Select a number from Register 1 line
-
There are two ways to do that:
- Random. In that case the program selects a random number out of the numbers displayed in Register 1. If you want that to happen select Random
- User controlled. In that case there are three options:
- You can select self a number out of row 9 and select Select
- In case there is a short list displayed starting from row 20, you can select one of those values and select
Select
- You can select a value either way, modify the value and select Select. The purpose is to see what happens what if values with smaller probabilities are selected.
In this particular case select in row 9 the value 4915 and select Select
-
Step 6 starts with the following 3 messages:
- Continued Fraction Convergent of 4915 . The value 4915 is the value selected at the end of Step 5
- In this particular case: Possible values for periodicity r, are multiples of r1 = 5
- In this particular case: GCD n = 55 a = 10 y = 34 p = 5 q = 11
The Debug Buffer shows the following text:
0 a = 0 p = 4915 / 8192
1 a = 1 p = 3277 / 4915 Convergent 1 / 1
2 a = 1 p = 1638 / 3277 Convergent 1 / 2
3 a = 2 p = 1 / 1638 Convergent 3 / 5
4 a = 1638 p = 0 / 1 Convergent 4915 / 8192
|
Accordingly, to the text: "We stop before the denominator exceeds n=55", that means that possible periodicity values are 5, 10, 15, 20, 25 etc.
You now have to perform the following calculations:
- 13^5 mod 55 = 43, 13^10 Mod 55 = 34, 13^15 Mod 55 = 13 and 13^20 mod 55 = 1
The last calculation means that periodicity is 20
Now a = 10. y = x^a mod n = 13^10 mod 55 = 34.
Finally you have two perform two calculations:
- GCD (y-1,n) = GCD(33,55) = 11
- GCD (y+1,n) = GCD(35,55) = 5
Together with this three Message two selection controls are displayed: Continue 7 and Repeat Step 5
- If you want to repeat the previous step: Select Repeat Step 5
Select 410 in row 9 and select Select
Observe that Continued Fraction Convergent (CFC) works.
- Again, Select Repeat Step 5 Change 410 into 406. Select 406 in row 9 and select Select CFC works.
- Again, Select Repeat Step 5 Change 406 into 400. Select 400 in row 9 and select Select CFC shows an error
Now select: Continue 7
For details see document 1 mentioned above.
-
At the end the following message is displayed This terminates Shor's Algorithm simulation
Finally, the factorization results of Classical Algorithm and Fermat's sieve Algorithm are displayed in resp. row 12 and row 13.
In this case the Classical Algorithm requires 3 calculations Fermat's sieve Algorithm requires 1 Calculation.
For Example: try 5 and 43 to observe that Shor's Algorithm has periodicity 84, Classical Algorithm requires 4 calculations and Fermat's Algorithm requires 10 calculations.
Finally select Continue 8 to start you next simulation.
1.4 Philosophical Discussion
In Step2 both the periodicity and the two prime numbers are calculated. This is possible because we study examples with very small prime numbers. In reality when you try very large numbers such an approach is not possible. The proposed solution is than to calculate the periodicity using a quantum computer. This is done in both step 3 (Measuring register 2) and step 5 (Measuring register 1). When this is done it is quite straightforward to calculate both the periodicity and the two prime numbers on a PC. However, and that is important, the algorithm does not always work.
The 2 Step approach is also followed in the spreadsheets: "Get Prime 1" and "Get Prime 2."
Still, it is a challenge to optimize this approach and to execute this using parallel programming. For more detail see:
1. Quantum Factoring Performance Evaluation - Using Parallel Processing - VB2010
2. Quantum Factoring Performance Evaluation - Using Parallel Processing - VB2019
Example 1 above closely resembles the operation of a quantum computer, however, and that is important, in a simulated environment. In reality a quantum computer operates in a physical environment and this environment is quite different. The issue is that when you compare the theoretical results (from the simulation) with the actual results the outcome should be the same.
In detail this means:
- Step 3 involves: "Measure Register 2." In this case with n = 55 the theorical results are a list of 20 numbers starting with: 1, 2, 4, 7, 8, 9 etc.
- The experimental outcome of one experiment of step 5 on a QC must be one of these 20 values.
- When you perform the same experiment, a 100 times, each of these specific values should be there roughly 5 times (and not any other number).
- Step 5 involves: Measure Register 1." The theoretical results with n = 55 are a list of 20 numbers starting with: 0, 410, 819, 1229, 1638 etc. Each value has a specific probability.
- The most probable experimental outcome of one experiment of step 5 on a QC should be one of these 20 values.
- When you perform the same experiment, a 1000 times, in 50 cases you should measure the value 0, in 12 cases 409, in 28 cases 410, in 2 cases 411, in 44 cases 819 etc
What this means that it is very time consuming to test if a QC works 100% correct.
2. Spreadsheet layout: "Get Pr1"
2.1 Program Operation: "Get Pr1", Button "Get Prime 1"
The Purpose of the spreadsheet is to calculate the two prime numbers pm1 and pm2 as a function of n. That means for different prime number combinations of pm1 and pm2.
The program displays the type (T1, T2, T3 or T4) and the periodicity as a function of each n.
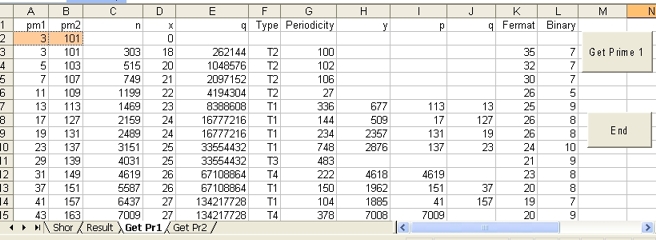
Input for the program are two (prime) numbers: pm1 and pm2. Those two numbers should be entered in the cells (2,A) and (2,B). After that select the button "Get Prime 1"
Those two numbers are used as start values for 50 prime number combinations. Multiplication of those two numbers gives a number n which is factorized 50 times using Shor's Algorithm in 2 steps.
As part of Step 1 for each of the 50 combinations the program displays the three calculated values n = pm1*pm2 in Cell (3,C) x in Cell (3,D) and q in Cell (3,E). q = 2^x
As part of Step 2 for each of the 50 combinations x^a mod n is calculated as a function of a. This calculation terminates when the result is 1 or is equal to any previous calculated value.
When the result is 1 the periodicity is equal to a. This value is stored in Cell (3,G).
- When the periodicity is even the calculation is of Type 1
-
- When the periodicity is odd the calculation is of Type 3. In that case Shor's Algorithm does not work.
-
- When the calculation detects any previous result not equal to 1 the calculation is of Type 2
-
Type is stored in Cell (3,E) as T1, T2 or T3.
For more detail go to Shor's Algorithm Answer Question 2.
What the spreadsheet shows is that the periodicity becomes very large and in worst cases is almost equal to: pm1*pm2/2. This challenges the usefulness of Shor's Algorithm.
2.2 Program Operation: "Get Pr1". Button "Get Prime 1" - Example 1
In order to understand the functionality of Get Prime 1 try the following three examples:
-
Enter: for pm1 = 3 and for pm2 = 5 and select the Button Get Prime 1
In this particular case n is a combination between two adjacent prime numbers.
Observe that most of factorizations are of type T1.
The last two columns show the number of calculations (loops) to perform
- The coloumn Fermat indicates the number loops to perform when factorization of the number n is done, using Fermat's factorization algorithm.
- The column Binary indicates Right-to-left binary method. The "Right-to-left binary method" is a part of Modular Exponentiation.. Modular Exponentiation is involved as part of Step 5 and Step 6 of Shor's Algorithm.
For more detail select: Shor's Algorithm Reflection 4 - Modular Exponentiation.
In this particular case all the values in the column Fermat are one and in column Binary are higher.
That means Fermats factorization algorithm out performs Shor's Algorithm.
-
Next try the prime numbers pm1 = 100 and pm2 = 200.
The fact that both numbers are not important because the program first calculates the two nearest prime numbers.
Observe that in all cases Fermat's factorization algorithm out performs Right-to-left binary method
-
The program also works for rather large prime number combinations.
- For example: try 1000 and 4000.
-
The largest periodicity value is 2000000.
Observe that in all cases Right-to-left binary method out performs Fermat's factorization algorithm
2.3 Program Operation: "Get Pr1". Button "Get Prime 1" - Example 2 n=283321
In order to understand the functionality of Get Prime 1 in more detail try the following example:
Enter: for pm1 = 300 and for pm2 = 900 and select the Button Get Prime 1
The fact that both numbers are not important because the program first calculates the two nearest prime numbers.
Observe line 4. This is the case when n=283321 and the two prime numbers are 311 and 911.
The number n is in this case of type 1 (this is a perfect example). That means that the number of values between the two stop signs (the number 1) is odd. That means that both the periodicity and the value y are easy to measure and or to calculate. For more detail go to Shor's Algorithm Answer Question 2.
The last two columns show the number of calculations (loops) to perform
- The coloumn Fermat indicates the number loops to perform when factorization of the number n is done, using Fermat's factorization algorithm.
- The column Binary indicates Right-to-left binary method. The "Right-to-left binary method" is a part of Modular Exponentiation.. Modular Exponentiation is involved as part of Step 5 and Step 6 of Shor's Algorithm.
For more detail select: Shor's Algorithm Reflection 4 - Modular Exponentiation.
In this particular case the two values in the columns Fermat and Binary are 79 and 15. That means Right-to-left binary method is the best and Shor's Algorithm wins.
However, it is not so simple as that. The number 15 is only valid when the period 28210 is measured. In that case Modular Exponentiation is only used once. This is true in 32% of the cases.
In the case when 4030 (or less) is measured (at least) 98 loops have to be performed. This is the case in 32% of the cases. In these cases, Fermat's factorization algorithm wins.
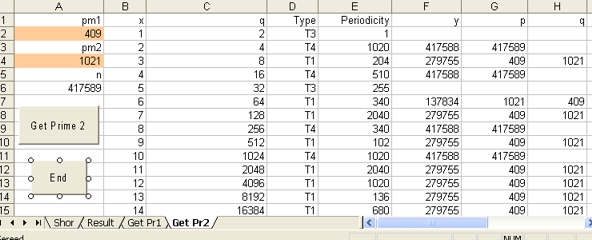
Observe line 40. This is the case when n=417589 and the two prime numbers are 409 and 1021.
The period is 408. The two values in the columns Fermat and Binary are 69 and 9.
408 is measured in 31% cases. 204 is measured in 16% cases.
In the case when 34 (or less) is measured (at least) 97 loops have to be performed. This is the case in 14% of the cases. Only in these cases, Fermat's factorization algorithm wins.
In the case when pm1=1000 and pm2=4000 in all cases Right-to-left binary method out performs Fermat's factorization algorithm. However, that does not mean that Shor's Algorithm implemented on a Quantum Computer also wins, because different hardware problems can be at stake. Study Shor's Algorithm 10 Questions
3. Spreadsheet layout: "Get Pr2", Button: "Get Prime 2"
3.1 Program Operation: "Get Pr2". Button: "Get Prime 2"
The Purpose of the spreadsheet is to calculate the two prime numbers pm1 and pm2 for a fixed value of n as a function of x. In this case x is going from 1 to 50
The program displays the type (T1, T2, T3 or T4) and the periodicity as a function of x
Input for the program are two (prime) numbers: pm1 and pm2. Those two numbers should be entered in the cells (2,A) and (4,A). After that select the button "Get Prime 2"
Those two numbers are used as start values for 50 prime number combinations. Multiplication of those two numbers gives a number n which is factorized 50 times using Shor's Algorithm in 2 steps.
The application "Get Prime 2" is specific written to study the article Oversimplifying quantum factoring in Nature. In this document of 11 July 2013 implementation constraints of Shor's Algorithm are discussed.
Feedback
None
Created: 19 April 2003
Modified 25 July 2013
Modified 14 November 2015
Modified 11 May 2023
Back to Shor's Algorithm - 10 Questions
Back to my home page: Contents of This Document