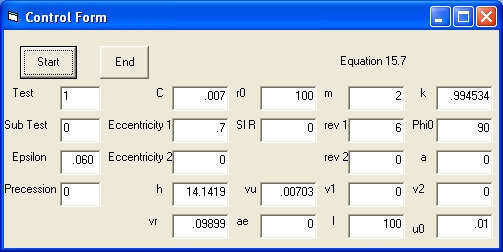
In order to control the excution of the program following control parameters are used:
- The parameter Test defines the test in progres. There are 7 tests. The parameter test can be entered directly. When the Label Test is selected the next test will be indicated.
- The parameter SubTest defines the subtest in progres. There are 6 subtests. The parameter subtest can be entered directly. When the Label SubTest is selected the next subtest will be indicated.
- The parameter Eccentricity defines the eccentricity (Ecc). The parameter is shown twice. The top one in Yellow is the requested value. The one below is the calculated value.
- The parameter l defines the Semi Latus Rectum . l = h^2/mu
See also https://en.wikipedia.org/wiki/Conic_section#Conic_parameters - The parameter m or mu defines the mass of the central object.
- The parameter k is used in the equations 15.23 (Test 5) and 15.24 (Test 4)
- The parameter rev 1 defines the number of revolutions of the point mass (Mercury).The parameter is shown twice. The top one rev 1 in Yellow is the requested value. The one below rev 2 is the calculated value.
- The parameter phi0 is the initial value of the angle phi.
Operation Test 1 - Select Start
After selecting Start the background color of 8 parameters will change in color Yellow. These fields represents the parameters that can be changed.- Change the parameter Rev 1 in Yellow from 6 to 3.
- Select: Contunue . This will perform test 1, which is Equation 15.7
- Observe that the parameter Eccentricity 2 will change to .7. This is the calculated Eccentricty,
The parameter "Sl R" = 99. This is the calculated Semi Latus Rectum.
Observe that the first revolution start at the distance "l". - When the test 1 is finished select "Start" and change the parameter test from 1 in to 1.2 and select "Continue".
- When the test 1.2 is finished select "Start" and change the parameter test to 1.3, 1.4 etc and select "Continue".
| Test | Ecc 1 | l | m | C | h | vr | vu | k | eps | Sl R |
| 1.1 | .7 | 100 | 2 | .007 | 14.1421 | .09899 | .00699 | .994534 | .060 | 99.99 |
| 1.2 | .5 | 100 | 2 | .005 | 14.1421 | .07071 | .00500 | .994534 | .060 | 99.99 |
| 1.3 | .3 | 100 | 2 | .003 | 14.1421 | .04242 | .00300 | .994534 | .060 | 99.99 |
| 1.4 | .7 | 150 | 2 | .007 | 17.3205 | .09899 | .00698 | .994534 | .040 | 149.99 |
| 1.5 | .7 | 200 | 2 | .007 | 20.0000 | .08082 | .00466 | .994534 | .030 | 199.99 |
| 1.6 | .7 | 100 | 1.5 | .007 | 12.2474 | .08573 | .00699 | .994534 | .044 | 100.00 |
| 1.7 | .7 | 100 | 3 | .007 | 17.3205 | .12124 | .00699 | .994534 | .090 | 99.99 |
- h = sqr(l * mu) or sqr(h = l * m)
- Epsilon = 3 * mu^2/ h^2
- vr = ecc * h / l. vr is used in equation 15.7
- vu = ecc / l. vu is used in equation 15.11 and 15.25
Test 1 Classical 15.7
Test 2 Classical 15.10
Test 2 is used to calculate the equation 15.10Equation 15.10 is the same as equation 15.25 (See test 3) with the factor "3 * mu^2" being equal to zero.
d^2u mu
------- + U = ---
d phi^2 h^2
Equation 15.10
|

|
Sub Test 1 Classical 15.11
mu
U = --- + C * cos(Phi - Phi0)
h^2
Equation 15.11
|

|
Sub Test 2 Classical 15.12
l
- = 1 + Ecc * (cos (Phi - Phi0))
R
Equation 15.12
|
|
Test 5 Mercury 15.23
|
|
|
Test 5 is a combination of the equations 15.21, 15.22 and 15.23. Equation 15.23 is the most difficult. This equation contains the two derivatives dr/dt^2 and dhi/dt^2. dhi/dt is calculated in equation 15.21. The derivative dr/dt^2 is called fac2. That means that dr/dt = sqr(fac2) The problem is that fac2 can become negative, which has to be taken into account. |
- Ecc (which is used to calculate h), l (which is used to calculate r0), m and k
| Test | Ecc | l | m | C | h | k | Epsilon | Precession |
| 5.1 | .7 | 100 | 2 | .007 | 14.1421 | .994534 | .060 | 25.65 |
| 5.2 | .6 | 100 | 2 | .006 | 14.1421 | .99318 | .060 | 25.65 |
| 5.3 | .5 | 100 | 2 | .005 | 14.1421 | .992045 | .059 | 25.65 |
| 5.4 | .4 | 100 | 2 | .004 | 14.1421 | .991112 | .059 | 25.65 |
| 5.5 | .3 | 100 | 2 | .003 | 14.1421 | .990412 | .060 | 25.65 |
| 5.6 | .7 | 100 | 3 | .007 | 17.3205 | .99145 | .090 | 43.80 |
| 5.7 | .7 | 100 | 4 | .007 | 20.0000 | .98802 | .120 | 67.41 |
| 5.8 | .7 | 100 | 1 | .007 | 10.0000 | .997301 | .030 | 11.76 |
- The tests 5.1, 5.2, 5.3, 5.4 and 5.5 show the different values for k when eccentricity decreases with m constant.
- The tests 5.1, 5.6, 5.7 and 5.8 show different values of m when eccentricity is constant
Test 4 Mercury 15.24
|
For i = 0 To imax
For j = 1 To di
Select Case test
Case Is = 4
' 15.24 page 196
C2 = 2
k1 = (k2 - 1) / h2 ' Eq 15.24
u2 = u * u
fac3 = k1 + u * (2 * m / h2 - u + C2 * m * u2)
If fac3 < 0 And Count = 0 Then
sign1 = sign1 * -1
Count = 1
End If
If sign1 = 1 Then kleur = LGreen Else kleur = Yellow
If Count > 0 Then
Count = Count + 1:
If Count >= maxcount Then Count = 0:
If sign1 = 1 Then kleur = LRed Else kleur = Black
End If
vu = sign1 * Sqr(Abs(fac3))
u = u + vu * ddPhi
r = 1 / u
phi = Phi00 * pi / 180 + i * dPhi + j * ddPhi
TESTMAXR eccr
If t2 > 0 Then t2 = 0
|
Test 3 Mercury 15.25
|
For i = 0 To imax
For j = 1 To di
Select Case test
Case Is = 2, 3
' 15.25 page 196
ac = m / h2 + C3 * m * u * u - u
vu = vu + ac * ddPhi
u = u + vu * ddPhi
r = 1 / u
phi = Phi00 * pi / 180 + i * dPhi + j * ddPhi
TESTMAXR eccr
If t2 > 0 Then t2 = 0
End Select
next j
' Display
xxx = r * Cos(phi)
yyy = r * Sin(phi)
px = px0 + fac * xxx
py = py0 - fac * yyy
Form2.PSet (px, py), QBColor(kleur)
next i
|
The function PSet stores one pixel on the display. The two previous equations 15.23 and 15.24 are much more difficult.
Test 6 Mercury 15.27
|
|
Test 7 Mercury 15.30
|
|
u0 is the initial value for u at t = 0
| test | C | r0 | m | k | ecc | ecc 2 | Pi0 | h | Epsilon | Precession |
| 7 | .007 | 100 | 2 | .994534 | .7 | 0 | 90 | 14.1421 | .060 | 0 |
| 7.1 | .0001 | 100 | 2 | .994534 | .01 | .7741 | 90 | 14.1421 | .060 | -4.677 |
Sub Test 3 Mercury 15.31
|
For i = 1 To imax
phi = Phi0 + i * dPhi + pi / 2
Select Case subtest
Case Is = 3
' equation 15.31
u0 = m / h2 * (1 + ecc * Cos(phi))
u1 = aa + bb * phi * Sin(phi) + CC * Cos(2 * phi)
u = u0 + Eps * u1
r = 1 / u
End Select
TESTMAXR eccr
If t2 > 0 Then t2 = 0
' Display
px = px0 + fac * r * Cos(phi):
py = py0 - fac * r * Sin(phi)
Form2.PSet (px, py), QBColor(kleur)
If maxcount = irev Then GoTo end1
If stop1 = 1 Then GoTo end2
Next i
|
| C | r0 | m | k | ecc | Pi0 | h | Epsilon | Precession |
| .007 | 100 | 1 | .994534 | .7 | 90 | 10 | .030 | 8.948 |
SubTest 4 Mercury 15.33
m d^2u h^2
u0 = --- * (1 + Ecc * cos(phi)) ---- + u = --- * u0^2
h^2 dt^2 m
Equation 15.33
|

|
| C | r0 | m | k | ecc | Pi0 | h | Epsilon | Precession |
| .007 | 100 | 1 | .994534 | .7 | 90 | 10 | .030 | 7.766 |
Sub Test 5 Mercury 15.34A
m
u0 = --- * [1 + Ecc * cos(phi) + Eps*Ecc*phi*sin(phi)]
h^2
Equation 15.34A
|

|
| C | r0 | m | k | ecc | ecc 2 | Pi0 | h | Epsilon | Precession |
| .007 | 100 | 1 | .994534 | .7 | .9262 | 90 | 10 | .030 | 7.941 |
Sub Test 6 Mercury 15.34B
m
u0 = --- * {1 + Ecc * cos[phi(1-Eps)]}
h^2
Equation 15.34B
|

|

|
Program Description
The program uses the following subroutines: Main and TESTMAXR. The subroutine Main is called when the Start Command is selected. The subroutine TESTMAXR is used to calculate the Perihelion (Shortest distance) and Aphelion (Farthest distance).Using that information, after 1 complete revolutions the parameters a, ae, v1 and v2 are calculated and displayed on the Control Form
Reflection 1
The starting point of the the different equations is to consider Mercury as a test particle. This is a very simple approach when you want to calculate the movements of the planets in the Solar System Using General Relativity.Of course you can claim that in order to perform such a simulation you can also use Newton's Law but than you will miss the precession of the perihelion.
A second issue is, and that is the most important issue, I want to investigate what is involved when you want to use GR. The main lesson is: It is already difficult just to perform a simplified example considering Mercury only. It will be extremely difficult when all planets are considerd, because they all interact which each other.
What makes numerical calculation difficult, specific for example equation 15.23 that the starting point should be to calculate the parameters and initial conditions using observations.
Specific you have to calculate the masses involved and the parameters h and k. The two parameters h and k are called constants, that may be true for each object (mass) involved, but in fact they are very important because they define the trajectory of each individual object. I expect you need as many parameter combinations (h,k) as objects involved
In the above I have calculated h directly from eccentricity but in general you cannot follow such an approach.
Observations in GR are specific difficult because proper time is used. GR does not use the concept of simultaneity, which makes the whole issue of observation "handling" difficult.
Reflection 2
The program is based using two concepts: Tests and Subtests. Tests are the numerical implementation of differential (or difference) equation. Subtests are the implementation of analytical solutions. Analytical solutions are functions in phi.All the implementations of tests (the differential equations 15.23, 15.24, 15.25 and 15.27) show the same result.
For the subtests this is different. That means the analytical solutions are not correct (except equation 15.34B). The same problem arises when you implement the algorithms show in the book "Astronomical Algorithms" by Jean Meeus. Using these algorithms (functions of t) you can calculate the position of the planet Mercury of any day in the future. However the accuracy is not enough to demonstrate the precession of the perihelion. It should be mentioned that nothing is wrong with this book: it is excellent. The same with the book "Astronomy with your personnal computer" by Peter Duffett-Smith.
Reflection 3
Paragaph 15.3 (Advance of the perihelion of Mercury) is an example of a one-body problem in general relativity. This is an extremely simple problem, because only one object (one mass) is considered. This is not even an realistic problem because any realistic problem studied should consists of at least 2 objects or masses.A much more realistic example consists of at least 3 objects: A BH at the center of our Galaxy, one star and one planet. That means at least 2 moving objects or two moving gravitational fields
Such an example shows much better the issues involved when you calculate a numerical solution using GR.
In order to study the behaviour of the planet Mercury also at least three objects should be involved.
Reflection 4
Numerical solutions require three steps. The first step involves observations. The second step consists of a pure mathematical process and the third step again involves observations, that means you have to test the result (predictions) of the mathematical process with actual observations in the future.The mathematical process consists of a mathematical description of the physical process studied. In our case a collection of astronomical objects.
In the first step and in the third step, because humans are involved to do the observations, light signals are involved. That means the speed and the trajectories of the photons is an issue. In step the most important parameter is the speed of the gravitational radiation.
This distinction at first side seems strange, but in reality the physical laws that govern the movement of astronomical objects and photons have nothing in common. In fact you should study these laws "with your eyes closed". The only exception comes when some of the objects involved (gas clouds) are electrical charged. In that sense you can make a distinction between baryonic and non baryonic matter but not between visible (which emits photons) and non visible or darkmatter.
Feedback
None
Created:1 September 2016
Back to my home page: Contents of This Document